dag xChoco,

waarop loop je vast in wat daar gegeven wordt in het correctievoorschrift?

Vanaf ''de spanningswet van Kirchhoff''

Ik wil niet vervelend doen, maar betekent dat dat je feitelijk geen idee hebt van wat de wetten van Kirchhoff voorstellen? 

Want in dat geval moeten we hier eigenlijk een complete kirchhoff-cursus gaan schrijven, da's niet in een vloek en een zucht gebeurd.
http://www.hhofstede.nl/modules/kirchhoff.htm

Er valt weinig aan te snappen: er zijn 2 wetten:

1. som van spanningen is nul langs een gesloten pad
Een gesloten pad langs een schakeling levert spanning 0 op (alles wat ergens bij komt in spanning, wordt elders weer (soms in andere verdelingen) weer afgehaald). Logisch als je weet dat spanning een indicatie voor de energie is die lading krijgt of afstaat (1V = 1J/C). Netto wordt alles wat aan energie gegeven wordt elders weer afgestaan.

2. Bij splitsingen geldt som van stroom in de takken is de totale stroom voor splitsing (ditto bij samenkomen)
Een stroom die zich splitst en verdeelt langs parallelle paden komt verderop weer bijeen tot dezelfde stroom. Vergelijk een weg die ineens dubbelbaans wordt en verderop weer eenbaans: het aantal auto's (stroom) is aan begin en eind weer hetzelfde (1A=1 C/s).

Daarmee moet je via allerlei paden in de schakeling kunnen beredeneren of er spanning tussen 2 punten van de schakeling staat en bij gevolg een stroompje loopt. Anders zou ik je boek nog eens goed doorlezen over elektriciteitsschakelingen.

Bedankt voor de reacties. Bij ons werd er gezegd dat we niet persé met de wetten van Kirchhoff hoefden te kunnen redeneren, vandaar. Ik zal de gegeven pagina eens doorlezen.

Ik heb het doorgelezen, maar ik begrijp de vergelijking bij lus 1 al niet, waarom moet je I3 er van af halen?

omdat als lusrichting met de klok mee is gekozen als positief. In die lus 1 loopt I₃ tegen die gekozen lusrichting in.

Dit soort info zou in V6 je toch geen problemen meer mogen geven... 

Bedankt Jan!

En Theo, dat zou het inderdaad niet, echter is bij ons altijd gezegd dat we nooit aan de hand van Kirchhoff hoeven te redeneren en aangezien het wel degelijk een nét iets andere manier van benaderen is, is het enigszins logisch dat het wat tijd vergt om dit allemaal in te zien, ondanks dat de regels van serie/parallelschakeling me wel duidelijk zijn.

Ik wist zelfs nieteens dat dit zo gevraagd kon worden, dan is het beter dat ik het al zie en er achter probeer te komen!

Wat gek zeg..Ik zit ook in 6V en dit hebben we nog nooit gehad. 

Huh ja ik ook! 

Het wordt al in 4V behandeld... tenminste door mij en de boeken. Maar zelfs als de naam onbekend is, dan nog gelden dezelfde regels voor spannings- en stroomberekeningen in gemengde schakelingen. Verschuil je niet achter de naam Kirchhoff (die pas sinds het vernieuwde examen dit jaar weer met name wordt genoemd net als de eenheid siemens voor geleidbaarheid (=Ω^-1)

Dat klopt inderdaad, bij ons werd verteld dat het eigenlijk precies de regels zijn die we al kenden (in 4V). We moesten dat van Kirchhoff maar laten zitten omdat je toch altijd met je bestaande kennis kon redeneren. Deze opgave zag er een beetje vreemd uit, door de net iets andere benadering!

Het is "gewoon" een schakeling waarbij je kunt/moet weten dat als 2 punten dezelfde spanning hebben er dan geen stroom loopt tussen die punten. Dus goed geschikt als een van de weerstanden wijzigt (rekstrook) waardoor de spanning niet meer hetzelfde is en er een stroom gaat lopen.

In soortgelijke situatie wordt de schakeling ook gebruikt om ipv rekstrook een onbekende weerstand te plaatsen en via een variabele weerstand (waarvan bekend is wat de weerstand telkens is) wordt geprobeerd weer een nulstroom te krijgen zodat de onbekende weerstand bepaald kan worden.

Bedankt voor de nadere toelichting, Theo!

Ik begrijp niet wat er gebeurt met de spanning over weerstand 2. (AD) Zou de spanning over weerstand 2 niet moeten dalen als deze over weerstand 1 stijgt? (de spanning wordt toch proportioneel verdeeld in een serieschakeling?)

Daarom begrijp ik niet waarom de stroom dan perse van B naar A gaat. Want de stroom van AD is toch ook gedaald? Ik hoop dat iemand me kan helpen.

Dag Lotte,

dat gebeurt ook hoor, wie of wat beweert van niet? 

groet, Jan

Niemand, alleen dan begrijp ik niet waarom de stroom van B naar A loopt. Want is het dan niet zo dat de stroom ook afneemt van A naar D? Dan kan het toch niet dat er stroom 'bijkomt'?

dag Lotte,

Als de spanning over AC stijgt betekent dat ook de spanning over BC moet stijgen, A en B staan immers weerstandsloos verbonden zullen dus altijd dezelfde potentiaal hebben. 

R3 is een vaste weerstand, het potentiaalverschil daarover kan slechts stijgen indien de stroom door R3 toeneemt t.o.v. de stroom door de even grote R4. 
En dat stroomsterkteverschil kan alleen ontstaan indien er stroom door de amperemeter gaat lopen.

groet, Jan

Volgens mij snap ik het nu, bedankt!

Dag allen,
In vraag 4 staat "Leg uit, gebruik makend van de wetten van Kirchhoff...". Dat is nogal zwaar geschut. Kan het niet wat eenvoudiger? Bij voorbeeld: als je Rrek in gedachten laat toenemen tot oneindig, kan de stroom alleen nog vanaf punt B naar R2 en R4; de stroom door R2 moet dus vanaf B naar A zijn gegaan.
De wetten van Kirchhoff zijn vooral interessant als we er met (combinaties van) serie en parallel niet meer uitkomen. Bij voorbeeld als de micro-ampèremeter een niet te verwaarlozen weerstand heeft. Dat leidt echter tot berekeningen die buiten het vwo-examenprogramma vallen.
Met vriendelijke groet,
Jaap Koole

dag Jaap,

dat vonden Theo, Willem en ik ook toen deze vraag vorig jaar hier langskwam, en hebben daar uitgebreid over gediscussieerd. Ik heb ook geen idee waarom men dat per se wil(de). Als dit niet een voorbeeldexamen maar een echt examen was geweest zou dat best tot heftige discussies in de examenbesprekingen hebben geleid denk ik, en tot grote en ongewenste verschillen van beoordeling door correctoren. 
Mag je hier, als het anders wordt aangepakt, wel correctieregel 3.3 (andere maar vaktechnisch correcte aanpak ook volledig goed rekenen) nu wel of niet toepassen omdat er nadrukkelijk om Kirchhoff wordt gevraagd....

groet, Jan

Dag Jan,
Je vraag kan ik niet eenduidig beantwoorden. Enerzijds kan men redeneren: "Kirchhoff is niet gebruikt, dus de vraag is niet beantwoord, dus geen scorepunt toekennen". Dat lijkt me te streng. Anderzijds kan men het antwoord beoordelen op vakinhoudelijke juistheid en 0...5 scorepunten toekennen.
Met vriendelijke groet,
Jaap Koole

Het is nou juist het doel van correctievoorschriften om de noodzaak over te gaan tot 'enerzijds, anderzijds' te voorkomen, zodat ook grote verschillen in beoordeling voorkomen worden. 

De bedoeling van de opgave is kennelijk te testen of een leerling Kirchhoff kan toepassen. Zoals we ook wel eens vragen "leg uit aan de hand van de grafiek of ...... " , om zijn/haar vaardigheid in gebruik van grafieken te testen, en dergelijke. Zonder Kirchhoff dus geen 3e en 4e scorepunt. Als iedere corrector dat zo doet is er niks aan de hand om iedereen een eerlijke en verdedigbare score toe te kennen.

Nog beter ware het om, als je dan per se Kirchhoff wil laten gebruiken, de vraag zó in te kleden dat hij zonder Kirchhoff niet of nauwelijks oplosbaar is. Vanuit dat gezichtspunt is dit dus simpelweg een slechte vraag. 

Groet, Jan

Hallo,

Hoe kan het dat Uab 0 is? Als er stroom loopt zou je toch verwachten dat het komt door een potentiaal? 

Dank.

dag Harold,

In theoretische zin heb je gelijk, helemaal 0 kan Uab niet zijn.

Maar vergelijk het met een bergriviertje dat door een smal dal met groot verval stroomt in een bergmeer, en na dat meer weer verder stroomt door een smal dal. Hoewel er per dag evenveel water door het riviertje stroomt als door het meer, vind je in die smalle dalen waarschijnlijk een verhang van misschien wel 100 meter per kilometer om voldoende water door zo'n smal dal te persen. Het verhang over het meer, heel nauwkeurig gemeten, is waarschijnlijk niet meer dan een enkele centimeter per kilometer. De stromingsweerstand in dat meer is dan ook duizenden keren kleiner dan de stromingsweerstand in de dalen.

De stromingsweerstand in ab is nagenoeg 0 . Er is dan ook nagenoeg geen spanning nodig om toch een stroom te kunnen hebben. En ga je supergeleidend, dan is er géén spanning nodig: breng  stroom op gang in een rondje door een supergeleidende schijf, en dan blíjft dat stromen ook nadat je de spanningsbron verwijderd hebt. 

$$ I = \frac{U}{R} $$  ingevuld bijvoorbeeld 0,000 001 V : 0,000 001 Ω   

In praktische termen, U=0, maar er stroomt nog steeds 1 ampère, een zeker niet verwaarloosbare stroomsterkte. 

Groet, Jan

Ja klopt maar ik heb wel een paar instanties gezien waar zo´n brugschakeling een significant resultaat in voltage heeft. Volgens mij is het niet gebruikelijk dat een Wheatstone brugschakeling een voltage tussen de twee punten A en B van 0 heeft.
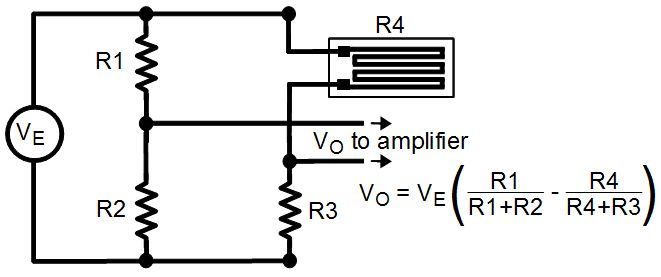
Ik heb even gegoogled wat de formule daarvoor is, waarbij R4 dus het rekstrookje voorstelt.

(R1 en R2 zijn in deze afbeelding R3 en R4 van de opgave.)

Dus R1 en R2 (oftewel R3 en R4 van opgave) zijn gelijk. Hierdoor  is de eerste term tussen de haken 0,5. De tweede term is dan bij waardes waarbij R4 (oftwel R1 van de opgave) dichtbij R3 zit -0,5. Hierdoor krijg je een spanning van bijna 0. Maar als R1 dus heel hoog wordt krijg je eigenlijk wel een spanning, want dan nadert de tweede term -1, en krijg je totaal dus -0,5 * Vbron.
Volgens mij zou je de vraag dan ook zo kunnen benaderen: Die V0 is in feite Va-Vb (als knooppunt-spanningen). Dus bij negatieve spanning is Vb groter dan Va en dus loopt het van b naar a. 

dat kan een doel van zo'n brugschakeling zijn, zoals in het geval dat je hierboven aankaart door een versterker aan weerszijden van de brug aan te sluiten, om een nog duidelijker uitlezing te krijgen.

In de oorspronkelijke opgave waarmee de topic begon hangen we er een micro-ampèremeter tussen. Die heeft (nagenoeg) geen weerstand en dus valt er (nagenoeg) geen spanning. 

Er zijn ook brugschakelingen waarbij R1 regelbaar is, en bij elke meting zo wordt ingesteld dat de stroom door de brug gelijk is aan 0 . Aan de positie van de regelbare weerstand kan dan de weerstand van R4 worden afgelezen.

En zo is er vast nog wel meer te bedenken.  

Maar dat doet niks af aan het antwoord op de eerdere vraagGroet, Jan

Hallo,

Die hele lage spanning in uw rekenvoorbeeld is toch alleen geldig bij het geval dat de weerstand die in de formule R4 is (dus het rekstrookje) heel dichtbij die 350 ohm zit? Zelfs als de meter geen weerstand heeft kan er volgens mij nog wel een spanningsverschil ontstaan in de knooppunten, als de regelbare weerstand bijvoorbeeld tot hoge waardes oploopt. De volgende site rekent bijvoorbeeld het spanningsverschil uit: http://www.daycounter.com/Calculators/WheatStone-Bridge/WheatStone-Bridge-Calculator.phtml

Bij waarde van Rx=350 ohm, inderdaad 0V. En zelfs bij 352 ohm nog 0,007V. Maar stel dat Rx= 380 ohm, dan heb je al gauw 0,1V. Aangezien ze niet vermelden hoeveel de weerstand verandert kan je toch eigenlijk niet met vaste zekerheid zeggen dat de spanning 0 blijft of 0 nadert?
De wet van Ohm zou je kunnen toepassen op het deel van de draad die de brug vormt maar dan zou je eigenlijk altijd U=0 krijgen bij verwaarloosbare weerstand, terwijl je volgens mij de potentiaal tussen de knooppunten A en B moet nemen om die spanning te krijgen en dan gaan de weerstanden R1,R2,R3 en R4 ook meewegen in die spanning over AB. 

Hopelijk kunt u mij aanwijzen waar ik een denkfout heb gemaakt.

Bedankt.

ja hoor :) 



en dat doet die site door tussen de punten  a en b een VOLTmeter te plaatsen: 





Die heeft een nagenoeg oneindig grote weerstand, er is dus geen verbinding tusen a en b . En dat is heel wat anders dan een ampèremeter, die je bijna mag beschouwen als een koperdraadje..

hier:
https://phet.colorado.edu/nl/simulation/legacy/circuit-construction-kit-ac-virtual-lab

kun je een java-applet downloaden en zelf je circuit met ampèremeter nabouwen. 
pas op, chrome weigert met java te werken, gebruik dus IE voor de download, en zorg dat je java geüpdated is. 
Kun je live de elektronen zien stromen, overal spanningen meten, en zien wat voor effect een verandering in je rekstrookje voor effecten heeft op stroom door ab, spanning over ab en spanning over alle andere weerstanden in dat circuit 





0,00000... V, toch een behoorlijke stroom......

Groet, Jan

Aha ik heb er even mee zitten puzzelen en nou zie ik de logica ervan in. Super bedankt! :)

Ja, die applet is goud waard, naar dat soort initiatieven  zou nou eens fors wat onderwijsbudget gestuurd moeten worden. Die ene applet is in zijn eentje al meer waard dan we hier in Nederland uitgeven aan onzin als rekentoetsen en zo. 

Maar goed, laten we er geen politieke topic van maken. 

groet, Jan

Dag allen,

De bedoeling van de oorspronkelijke vraag "Leg uit ... Kirchhoff ... in welke richting ..." is vermoedelijk niet geweest dat leerlingen zo diep graven (of zoveel gaan rekenen) als hier in sommige berichten gebeurt. Heeft de maker van de opgave het probleem dan wel zo gepresenteerd en de vraag zo gesteld dat de leerling gaat doen wat men redelijkerwijs kan verlangen?

Jan noteert: "De stromingsweerstand in ab is nagenoeg 0". Tussen A en B is een micro-ampèremeter getekend. Die bestaan in allerlei soorten. Vaklui gebruiken in sommige situaties zo'n goeie ouwe analoge wijzermeter als
www.simpsonelectric.com/images/File/datasheets/2608xi.pdf

Volgens de tabel "DC current" op p2 staat over dit instrument een spanning van circa 0,250 V als we hem gebruiken in het bereik van 50 micro-ampère. Dat komt neer op een weerstand in de orde van van 5000Ω, dus niet verwaarloosbaar ten opzichte van 350Ω. Dat een meter voor stroomsterkten in de orde van 1 A een lage weerstand heeft, komt doordat het leeuwendeel van die stroom dan door een shuntweerstand in de meter gaat en niet door de draaispoel. Hoe het zit bij een digitale micro-ampèremeter, is me niet bekend.

Als we aannemen dat de micro-ampèremeter een constante weerstand van 5000Ω heeft, geven de wetten van Kirchhoff over de meter een spanning U_AB=0,017V bij R_rek=360Ω en U_AB=0,97V bij R_rek=1350Ω. Zulk rekenwerk kan zeker niet worden verlangd als zo'n opgave in een centraal examen verschijnt.

In alle gevallen loopt de stroom inderdaad van A naar B. Om dat uit te leggen hebben we de wetten van Kirchhoff niet nodig, lijkt me.

Met vriendelijke groet,
Jaap Koole

dag Jaap,

wat ook de bedoeling van die examenvraag geweest moge zijn, hij is door sommigen aangegrepen om dieper op de principes in te gaan. Harold snapt nu dat ook indien ab een weerstandsloze en dus spanningloze verbinding zou zijn er tóch stroom zal kunnen lopen. 

Je toevoeging dat een echte micro-ampèremeter niet weerstandsloos is voegt aan dat algemene begrip alleen maar toe.

Over de oorspronkelijke voorbeeldexamenvraag gaat het al lang niet meer. Op zich een goede zaak, want we waren het ook al lang erover eens dat die vraag niet de beste examenvraag is die we ooit gezien hebben. Desalniettemin, petje af voor de collega's die elk jaar toch weer een zak verrassend originele oefeningen, vaak van wél hoge kwaliteit, open weten te trekken. 

groet, Jan

hallo, 

waarom neemt de spanning over R1 toe. Het is toch dat bij een toename van de weerstand dat de stroomsterkte afneemt?

Het rekstrookje krijgt een hogere weerstand, de andere weerstand houdt zijn waarde.
Over beide weerstanden staat de batterijspanning, U = I(R1+R2) = IR1 + IR2
Ongeacht hoeveel stroom er door de weerstand loopt, is de verhouding tussen de spanning over elk van de weerstanden   U1/U2 = IR1/IR2 = R1/R2  evenredig met de weerstand.
Als weerstand R1 toeneemt dan neemt dus ook de spanning U1 over R1 toe. Tegelijk neemt U2 af zodat ze samen toch batterijspanning U overbruggen.

hallo Theo, 

ik denk dat ik het nu snap, dankjewel!