Golflengte en trillingstijd
Twen stelde deze vraag op 13 september 2015 om 10:10. Hallo,
Klopt het dat 1 trillingstijd gelijk is aan de golflengte bij golven (bijv. geluid) die je zichtbaar maakt met een oscilloscoop? Dus 1 hele trilling is van top tot de volgende top en dat is weer de golflengte.
Groeten, Twen
Reacties
Jaap
op
13 september 2015 om 12:10
Dag Twen,
Je gedachtegang is juist, maar je kunt het beter anders zeggen.
De trillingstijd is de tijdsduur van een trilling: van de top tot de top op het scherm van de oscilloscoop. Dat zie je goed. Die horizontale afstand op het scherm heet niet een "golflengte" maar de trillingstijd.
Wat je ziet op het scherm is niet een "golf", maar een grafiek van de uitwijking (spanning, verticaal) als functie van de tijd (horizontaal).
Een golf zie je bij voorbeeld als een berg en een dal op een flitsfoto van een strak gespannen springtouw. Dat is iets anders dan hetgeen je op de oscilloscoop ziet.
Oscilloscoop: een grafiek van een trilling met de tijd horizontaal.
Foto van een touw: je ziet alle punten op één tijdstip.
Groeten,
Jaap Koole
Je gedachtegang is juist, maar je kunt het beter anders zeggen.
De trillingstijd is de tijdsduur van een trilling: van de top tot de top op het scherm van de oscilloscoop. Dat zie je goed. Die horizontale afstand op het scherm heet niet een "golflengte" maar de trillingstijd.
Wat je ziet op het scherm is niet een "golf", maar een grafiek van de uitwijking (spanning, verticaal) als functie van de tijd (horizontaal).
Een golf zie je bij voorbeeld als een berg en een dal op een flitsfoto van een strak gespannen springtouw. Dat is iets anders dan hetgeen je op de oscilloscoop ziet.
Oscilloscoop: een grafiek van een trilling met de tijd horizontaal.
Foto van een touw: je ziet alle punten op één tijdstip.
Groeten,
Jaap Koole
Jan van de Velde
op
13 september 2015 om 16:38
dag Twen,
De twee grafieken die Jaap noemt lijken oppervlakkig bekeken als twee druppels water op elkaar. Maar er is een belangrijk verschil-
Op een oscilloscoop zie je de uitwijking VAN ÉÉN PUNT van de golf OP ALLE TIJDSTIPPEN.
In andere woorden, de uitwijking is uitgezet tegen de tijd (t) .
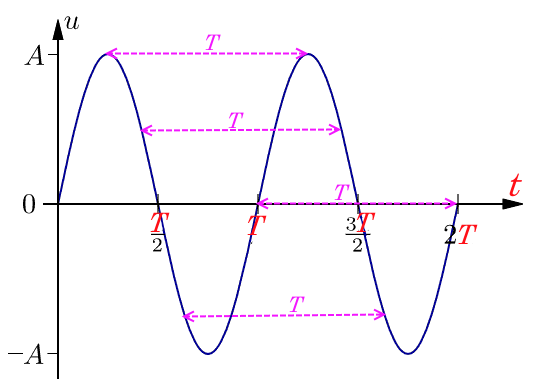
In zo'n oscilloscoopgrafiek kun je dus ook de trillingstijd (dat is per slot van rekening een soort tijd) aflezen tussen allerlei welgekozen punten op zo'n grafiek, want horizontaal staat de tijd uitgezet. Maar een golflengte kun je hier niet aflezen, net zo min als je in een temperatuurgrafiek van De Bilt de windsnelheid kunt aflezen.
Maar ik kan ook zoals Jaap zegt een foto maken van een golf, en dan zie ik de uitwijking VAN ALLE PUNTEN van de golf OP ÉÉN TIJDSTIP.
In andere woorden, de uitwijking is uitgezet tegen de plaats (x).

In zo'n plaatsgrafiek kun je dus ook de golflengte (dat is per slot van rekening een soort afstand) aflezen tussen allerlei welgekozen punten op zo'n grafiek, want horizontaal staat de plaats uitgezet.
Nou lijken beide bovenstaande grafiekjes wel fotokopieën van elkaar maar dat is maar schijn. Zou het bijvoorbeeld gaan om een geluidsgolf met een frequentie van 3400 Hz dan is λ ongeveer 0,1 m (onderste grafiek) en T ongeveer 0,0003 s.
maar dat is maar schijn. Zou het bijvoorbeeld gaan om een geluidsgolf met een frequentie van 3400 Hz dan is λ ongeveer 0,1 m (onderste grafiek) en T ongeveer 0,0003 s.
Is er tóch een verband tussen? Ja.
Het verband tussen f en T ken je wel: f=1/T
Een ander vrij bekend verband is v=λ·f
Combineer die twee verbanden tot v=λ/T en dan zie je dat je VIA die golfsnelheid v met de T uit een oscilloscoopgrafiek toch ook de golflengte λ kunt berekenen. Nog steeds niet rechtstreeks aflezen natuurlijk, maar zo blijkt er toch wel een duidelijk verband te zijn tussen beide grafieken.
Groet, Jan
De twee grafieken die Jaap noemt lijken oppervlakkig bekeken als twee druppels water op elkaar. Maar er is een belangrijk verschil-
Op een oscilloscoop zie je de uitwijking VAN ÉÉN PUNT van de golf OP ALLE TIJDSTIPPEN.
In andere woorden, de uitwijking is uitgezet tegen de tijd (t) .

In zo'n oscilloscoopgrafiek kun je dus ook de trillingstijd (dat is per slot van rekening een soort tijd) aflezen tussen allerlei welgekozen punten op zo'n grafiek, want horizontaal staat de tijd uitgezet. Maar een golflengte kun je hier niet aflezen, net zo min als je in een temperatuurgrafiek van De Bilt de windsnelheid kunt aflezen.
Maar ik kan ook zoals Jaap zegt een foto maken van een golf, en dan zie ik de uitwijking VAN ALLE PUNTEN van de golf OP ÉÉN TIJDSTIP.
In andere woorden, de uitwijking is uitgezet tegen de plaats (x).

In zo'n plaatsgrafiek kun je dus ook de golflengte (dat is per slot van rekening een soort afstand) aflezen tussen allerlei welgekozen punten op zo'n grafiek, want horizontaal staat de plaats uitgezet.
Nou lijken beide bovenstaande grafiekjes wel fotokopieën van elkaar
 maar dat is maar schijn. Zou het bijvoorbeeld gaan om een geluidsgolf met een frequentie van 3400 Hz dan is λ ongeveer 0,1 m (onderste grafiek) en T ongeveer 0,0003 s.
maar dat is maar schijn. Zou het bijvoorbeeld gaan om een geluidsgolf met een frequentie van 3400 Hz dan is λ ongeveer 0,1 m (onderste grafiek) en T ongeveer 0,0003 s. Is er tóch een verband tussen? Ja.
Het verband tussen f en T ken je wel: f=1/T
Een ander vrij bekend verband is v=λ·f
Combineer die twee verbanden tot v=λ/T en dan zie je dat je VIA die golfsnelheid v met de T uit een oscilloscoopgrafiek toch ook de golflengte λ kunt berekenen. Nog steeds niet rechtstreeks aflezen natuurlijk, maar zo blijkt er toch wel een duidelijk verband te zijn tussen beide grafieken.
Groet, Jan
Twen
op
13 september 2015 om 19:02
Bedankt voor de uitleg. Oke. Maar als je zegt dat 1 trilling van top tot top is dan kun je ook weer snel zien wat de frequentie (aantal trillingen per seconde) is toch?
Jan van de Velde
op
13 september 2015 om 19:21
Zien niet, even snel berekenen wel.
