luchtweerstand Cw-waarde berekenen
Jourens stelde deze vraag op 15 december 2009 om 17:17.Voor ons profielwerkstuk hebben we een auto op schaal gemaakt.
wij wilden aan de hand van dit schaalmodel de luchtweerstand berekenen. De formule voor de luchtweerstand is:
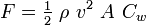 waarin:F = kracht die de weerstand tijdens de beweging ondervind.ρ = dichtheid van de stof, waarin beweegt.V = snelheid ten opzichte van het medium waarin het zich bevindt.A = geprojecteerd oppervlakte loodrecht op de beweegrichtingCw = weerstandscoëfficiënt De dichtheid, snelheid en opp zijn bekend. Er zijn nog 2 onbekenden. Hoe kan ik deze berekening dan uitvoeren?
waarin:F = kracht die de weerstand tijdens de beweging ondervind.ρ = dichtheid van de stof, waarin beweegt.V = snelheid ten opzichte van het medium waarin het zich bevindt.A = geprojecteerd oppervlakte loodrecht op de beweegrichtingCw = weerstandscoëfficiënt De dichtheid, snelheid en opp zijn bekend. Er zijn nog 2 onbekenden. Hoe kan ik deze berekening dan uitvoeren? (misschien met proefopstelling, maar hoe?)
alvast bedankt,
Jourens
Reacties
Ik wil graag de Cw waarden uitrekenen. Er zijn geen andere methoden om deze te bepalen? zijn er geen standaard waarden bekend?
Dan had ik nog een vraag. Heeft een recht oppervlakte cwwaarde 1? en hoe veranderd dat bij een hoek van 45 graden naar achteren (over horizontale as)?
Alvast hartelijk bedankt,
Jourens
Er zijn best wel standaardwaarden bekend (gemeten in windtunnels) maar dat is dan voor allerlei voorwerpen met standaardvormen. Elke vorm, met uitsteeksels en al, heeft zo zijn eigen Cw-waarde, dus behalve met meten is daaraan niets te voorspellen, ook niet voor jouw speelgoedauto. Auto- en vliegtuigfabrikanten meten in windtunnels ook de Cw van hun modellen.
Een lijstje vind je hier:
http://en.wikipedia.org/wiki/Drag_coefficient
Groet, Jan
Die komt uit de formule voor drukverliezen in stromende vloeistoffen of gassen van Bernoulli.
zie hier de afleiding:
https://physics.info/drag/
Groet, Jan
Ik doe een zelfstandig onderzoek en mijn onderzoeksvraag is wat de stroomlijncoefficient is van een kegel, oftewel Cw. Inmiddels weet ik dat dat 0,5 is, alleen moet ik dat in een proef laten zien. Ik heb al de maximale snelheid berekend van de kogels, zodat Fw=Fz, maar ik ben nog een beetje radeloos over wat ik nu moet doen.
Moet ik de Fz berekenen en is daar een specifieke formule voor om de zwaartekracht op een kegel te bereken?
Alvast bedankt!
De wrijvingskracht in de lucht bij het vallen is wel heel afhankelijk van de vorm: een potlood dat met de punt in de valrichting valt heeft veel minder wrijving dan een potlood dat horizontaal liggend valt. Een kegel met de punt in de valrichting heeft ook minder weerstand dan de ronde onderkant eerst laten vallen.
Bij vaste eindsnelheid is weliswaar Fzw = Fwrijving maar dat kan dus nogal schelen afhankelijk van hoe de kegel valt...
Angelique plaatste:
..//.. moet ik dat in een proef laten zien.hier:
https://www.natuurkunde.nl/vraagbaak/58724
vind je alvast een paar tips.
groet, Jan
Dat is niet waar. Kracht = massa x versnelling.
Bij constante vertikale snelheid is er geen kracht want geen versnelling. Bij berekening van luchtweerstand mag dit zo lijken te zijn (evenredig met v2) maar deze snelheid wordt bereikt door de zwaartekracht (die laat de snelheid toenemen) en de grootte van de luchtweerstand kun je berekenen maar het effect is nog steeds a=F/m : het voorwerp verandert van snelheid. Was er geen (zwaarte)kracht geweest die snelheid doet toenemen, dan was er ook geen luchtweerstand en bleef v=0 m/s
massa x zwaartekracht Is geen kracht (eenheid Nkg). Hier wordt ook van alles door elkaar gehaald.
Iets valt door de zwaartekracht. De grootte is massa x valversnelling = mg (en g is niet "de zwaartekracht").
Doordat een voorwerp versnelt neemt de snelheid toe en daarmee de luchtweerstand die blijkt evenredig met v2 te zijn. Die gaat de zwaartekracht tegenwerken. Tot het moment dat de luchtweerstand en zwaartekracht even groot en tegengesteld zijn: dan is er netto geen kracht meer. Daarmee ook geen versnelling: de eindsnelheid is constant.
Maar er zijn wel 2 gelijk grote en tegengestelde krachten waarbij de luchtweerstand ontstaat door de zwaartekracht die een voorwerp wil versnellen. Geen zwaartekracht (geen versnelling) dan ook geen luchtweerstand (voorwerp blijft met v=0 m/s stil liggen). Beweegt het wel door een eigen motor? Dan levert die een kracht waardoor het voorwerp sneller gaat en daarmee weer een luchtweerstand ondervindt. Zoals bijv een rijdende auto. Die ondervindt steeds meer wind en zal ooit een maximum snelheid bereiken als motorkracht en luchtweerstand elkaar precies tegenwerken met resultaat 0 N.
In de twee grafieken hieronder zie je hoe een weggeslagen tennisbal (schuin omhoog) eerst een hoge snelheid heeft en dan ook een grote wrijvingskracht, daarna de snelheid afneemt tot bij het hoogste punt er alleen nog horizontale snelheid is (en veel minder wrijving) en dan bij het vallen de snelheid (horizontaal en vertikaal) weer toeneemt en daarmee ook de wrijving. Alleen is op een gegeven moment de wrijving (omhoog) even groot als de zwaartekracht (naar beneden) en vanaf dat moment is de snelheid constant en de wrijving ook.

groetjes Swieber
Ik zou voor een pws ook eens goed naar je Nederlands kijken want dat laat in 3 regels voor de vraag ook te wensen over.
Hoe je de luchtweerstandscoëfficiënt Cw kunt berekenen, hangt af van je gegevens.
Welke gegevens of gemeten waarden heb je?
Taal en spelling: we schrijven 'de luchtweerstandscoëfficiënt'
en niet 'het luchtweerstand coeficient'.
Groet, Jaap
Je kunt de Cw waarde ook bepalen met een andere proefopstelling dan een windtunnel. Dat is wellicht makkelijker te realiseren. Je kunt het medium veranderen in water ipv lucht. Vervolgens maak je een hoge koker/cilinder gevuld met water. Het object waar je de Cw waarde van wilt bepalen kun je dan laten stijgen of dalen in deze cilinder. De kracht waarmee het stijgt of daalt kun je berekenen door de massa en volume van het object te bepalen. Daarmee bereken je de resultante van opwaartse kracht en zwaartekracht. Vervolgens hoef je in je meetopstelling alleen nog maar de v te bepalen waarop F waterweerstand (ipv luchtweerstand) gelijk is aan de F resultante van opwaartse en zwaartekracht. Nog even het geprojecteerde oppervlak (A) bepalen, en dan ben je klaar om Cw te kunnen berekenen.
Moet je wel nog even bedenken hoe je de snelheid onder water kunt berekenen. Daar is ook wel een opstelling voor te maken, bijv door een dun draadje aan je object te verbinden, en boven water de snelheid te bepalen van een eraan gekoppeld draaiwieltje. Of iets met een afstandmeter.
