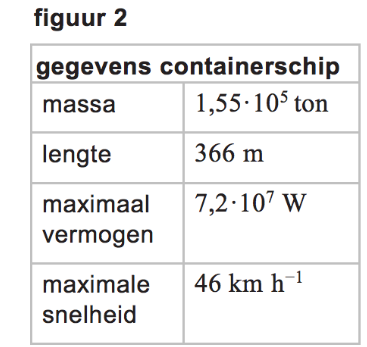
In 2017 liep een groot containerschip op de oever van de Schelde. Een onderzoeker deed onderzoek naar dit ongeluk. Hij zag dat het schip over een afstand van 50% van zijn lengte op de oever was geschoven. Zie figuur 1. Op internet zijn de gegevens van het schip te vinden. Zie figuur 2.

Bron: Wikimedia Commons
Van ieder schip wordt elke 2 minuten de positie bijgehouden. Met deze informatie bepaalde de onderzoeker de snelheid van het schip voor het ongeluk. Die bleek $7,1\,ms^{-1}$ te zijn. Hij ging ervan uit dat de wrijvingskracht op het schip tijdens het vastlopen op de oever constant was. Hij berekende dat die wrijvingskracht $2,1\cdot 10^{7}N$ was.
a. Toon met behulp van arbeid en kinetische energie aan dat deze waarde voor de wrijvingskracht klopt.
Voor de kinetische energie van het schip vóór het afremmen geldt: $E_{k}=\frac{1}{2}mv^{2}=\frac{1}{2}\cdot 1,55\cdot 10^{8}\cdot 7,1^{2}=3,91\cdot 10^{9}J$ . Het schip heeft afgeremd over een afstand van $0,50\cdot 366=183m$ . Hieruit volgt voor de wrijvingskracht: $\left(E_{k}\right)W=F_{w}\cdot s\to F_{w}=\frac{W}{s}=\frac{3,91\cdot 10^{9}}{183}=2,1\cdot 10^{7}\left(N\right)$ .
| gebruik van $W=\Delta k$ met $E_{k}=\frac{1}{2}mv^{2}$ | 1 punt |
| inzicht dat $s=0,50\cdot l_{schip}$ | 1 punt |
| gebruik van $W=F\cdot s$ | 1 punt |
| completeren van de berekening | 1 punt |
Met de gegevens uit figuur 2 kan de maximale kracht van de motor berekend worden. De onderzoeker concludeerde uit deze berekening dat de wrijvingskracht te groot was en het schip met de eigen motor niet los kon komen van de oever.
b. Toon met een berekening aan dat die conclusie klopt.
Er geldt: $P_{moter,max}=F_{moter,max}\cdot v_{max}\to 7,2\cdot 10^{7}=F_{moter,max}\cdot\frac{46}{3,6}\to $ $F_{moter,max}=5,6\cdot 10^{6}N$ . Deze motorkracht is kleiner dan de wrijvingskracht op het schip.
| gebruik van $P=F\cdot v$ | 1 punt |
| completeren van de berekening | 1 punt |
| inzicht dat de motorkracht vergeleken moet worden met de wrijvingskracht op het schip | 1 punt |
Er werden duwboten ingezet om het schip los te duwen van de oever. Zie figuur 3. De duwboten duwden eerst het schip aan de achterkant opzij. Het schip is hierbij als hefboom te beschouwen. Om 19.00 uur begonnen de duwboten te duwen, het schip lag toen nog stil. Een paar minuten later begon het schip om een punt te draaien dat met D is aangegeven.

Op de uitwerkbijlage is de situatie van 19.00 uur, zoals getekend in figuur 3, vergroot weergegeven. In de figuren op de uitwerkbijlage zijn het aangrijpingspunt W van de wrijvingskracht Fw en het aangrijpingspunt B van de totale duwkracht Fduwboten weergegeven.

c. Voer de volgende opdrachten uit: i) Teken in de figuren op de uitwerkbijlage de armen van Fw en Fduwboten.

| intekenen van de armen van de krachten | 1 punt |
ii) Leg met behulp van de hefboomwet uit of om 19.00 uur de totale duwkracht Fduwboten groter was dan Fw, kleiner was dan Fw of even groot was als Fw.
De arm van de kracht van de duwboten is langer dan de arm van de wrijvingskracht. De momenten zijn gelijk, dus uit de hefboomwet volgt dan dat de totale duwkracht van de duwboten kleiner was dan de wrijvingskracht.
| inzicht dat de arm van de duwkracht groter is dan de arm van de wrijvingskracht | 1 punt |
| gebruik van de hefboomwet en consequente conclusie | 1 punt |
Om het schip los te duwen, moesten de duwboten de wrijvingskracht tussen het schip en de oever overwinnen. Deze wrijvingskracht is evenredig met de normaalkracht van de oever op het schip. Behalve de normaalkracht werkte er ook een opwaartse kracht van het water op het schip. Zie schematisch en niet op schaal weergegeven in figuur 4. Hoe dieper een schip in het water ligt, hoe groter deze opwaartse kracht is.

Tijdens opkomende vloed (hoogwater) begon het water in de Schelde te stijgen.

d. Omcirkel in de tabel wat er gebeurde tijdens het stijgen van het water.

| de eerste twee regels juist | 1 punt |
| de derde regel consequent met de tweede | 1 punt |
