Een gasbarbecue gebruikt gas uit een stalen gasfles als energiebron. Zie figuur 1 hieronder
Bron: Wikimedia Commons
Hans en Sanne doen onderzoek naar verschillende methodes om te bepalen hoe vol een stalen gasfles is. Een lege gasfles kan gevuld worden met maximaal 6,1 kg vloeibaar propaan. Hans en Sanne hebben een barbecue met een vermogen van 15 kW. De stookwaarde van vloeibaar propaan is 13,8 $\textup{kWh} \textup{ kg}^{-1}$
a. Bereken hoelang de barbecue kan branden als begonnen wordt met een volle gasfles. Noteer je antwoord in het juiste aantal significante cijfers.
Er geldt: $E_{ch} = r_m m = 13,8 \cdot 6,1 = 84,2\textup{ kWh}$
De tijd dat de barbecue hier op kan branden is:
$t = \frac{E}{P} = \frac{84,2}{15} = 5,6\textup{ h} (= 2,0 \cdot 10^4 \textup{s})$ .
| gebruik van $E_{ch}=r_{m}\cdot m$ | 1 punt |
| gebruik van $E=P\cdot t$ | 1 punt |
| completeren van de berekening | 1 punt |
| significantie | 1 punt |
Ze merken dat na een tijd barbecueën de buitenzijde van de fles koud aanvoelt en dat er waterdruppels op de fles ontstaan. Ze beredeneren dat het vloeistofpeil van het propaan ongeveer gelijk moet staan aan de bovenrand van de waterdruppels op de fles. Ze concluderen dat de fles afkoelt door de faseovergang van het propaan in de fles van vloeibaar
naar gasvormig.
b. Hieronder staan twee zinnen, omcirkel in elke zin het juiste antwoord.
i. De faseovergang van vloeibaar naar gasvormig propaan in de fles heet: smelten / stollen / verdampen / condenseren / sublimeren.
ii. De faseovergang van waterdamp naar waterdruppels op de buitenzijde van de fles heet: smelten / stollen / verdampen / condenseren / sublimeren.
i. De faseovergang van vloeibaar naar gasvormig propaan in de fles heet: smelten / stollen / verdampen / condenseren / sublimeren.
ii. De faseovergang van waterdamp naar waterdruppels op de buitenzijde van de fles heet: smelten / stollen / verdampen / condenseren / sublimeren.
| juiste faseovergang | 1 punt |
| juiste faseovergang | 1 punt |
Wanneer Hans tegen de gasfles slaat, produceert deze een toon. Hij vraagt zich af of deze toon afhankelijk is van de vulstand van de fles. Tijdens het vullen van een fles bepaalt Hans de frequentie van de grondtonen die de gasfles produceert bij verschillende vulstanden, van leeg tot vol. Hiervan maakt hij een diagram. Hierin is de vulstand als percentage weergegeven. Zie het figuur hier onder.

Bij elke vulstand is er een laag gas boven de vloeistof. Hans denkt dat de tonen ontstaan door een staande golf in dit gas. Zie schematisch in het figuur hier onder.

c. Leg met behulp van figuren 2 en 3 uit dat Hans ongelijk heeft.
In figuur 2 is te zien dat de gemeten frequentie van de toon afneemt tijdens het vullen. Echter, in figuur 3 is te zien dat de golflengte van een staande golf in het propaangas zou afnemen tijdens het vullen. Hoe korter de golflengte, hoe hoger de frequentie van het geluid moet worden (bij gelijkblijvende geluidssnelheid).
| inzicht dat de frequentie afneemt bij het vullen van de fles | 1 punt |
| inzicht dat bij het vullen van de fles de golflengte kleiner zou worden | 1 punt |
| inzicht in het verband tussen frequentie en golflengte | 1 punt |
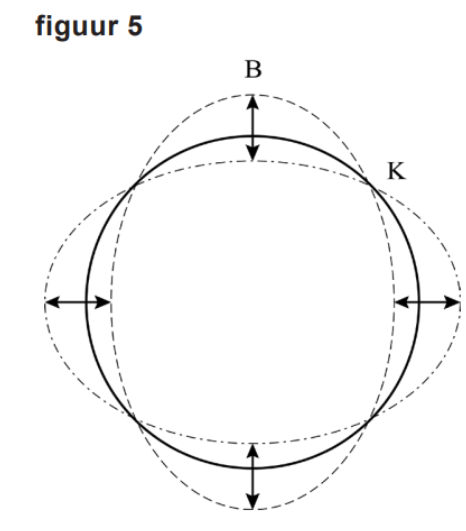
Sanne heeft een andere verklaring voor de toon. Zij denkt dat de gasfles zelf als een soort snaar werkt. Op de omtrek van de gasfles ontstaat dan een staande golf met vier knopen K en vier buiken B, net als bij een trillend wijnglas. Zie figuur 4 en schematisch in figuur 5.
De gasfles is gemaakt van staal en heeft een omtrek van 72 cm. De frequentie van de toon van de lege gasfles is $1,50 \cdot 10^3\textup{ Hz}$ .
d. Toon met een berekening aan of de golfsnelheid in de verklaring van Sanne gelijk is aan de voortplantingssnelheid van geluid in staal bij kamertemperatuur.
Er passen 2 golflengtes op de omtrek van de fles.
Dus: $\lambda = \frac{l}{2} = \frac{0,72}{2} = 0,36 \textup{ m}$ .
Hieruit volgt $v = f \lambda = 1,50 \cdot 10^3 \cdot 0,36 = 5,4 \cdot 10^2\textup{ ms}^{-1}$ .
De voortplantingssnelheid van geluid in staal is $5,1 \cdot 10^3 \textup{ ms}^{-1}$ (Binas) of $5,79 \cdot 10^3 \textup{ ms}^{-1}$ (Sciencedata). De golfsnelheid is dus niet gelijk aan de voortplantingssnelheid in staal.
| inzicht dat $\lambda=\frac{l}{2}$ | 1 punt |
| gebruik van $v=f\cdot\lambda $ | 1 punt |
| opzoeken van vstaal | 1 punt |
| completeren van de berekening en consequente conclusie | 1 punt |
Hans en Sanne proberen of ze met behulp van figuur 2 de vulstand van een gedeeltelijk gevulde gasfles kunnen bepalen. Ze gebruiken een oscilloscoop-app. Met hun telefoon maken ze een oscillogram van de toon die ontstaat door het aanslaan van de fles. Zie het screenshot in figuur 6.

e. Bepaal met behulp van figuren 2 en 6 de vulstand (in %) van deze gasfles. Noteer je antwoord in twee significante cijfers.
Er worden 20,5 trillingen geproduceerd tussen 4,0 ms en 20,0 ms, dus
$T = \frac{20,0 \cdot 10^{-3}-4,0\cdot 10^{-3}}{20,5} = 7,80 \cdot 10^{-4} \textup{ s}$ .
Voor de frequentie geldt: $f = \frac{1}{T} = \frac{1}{7,80 \cdot 10^{-4}} = 1,28\cdot 10^3 \textup{ Hz}$ .
Aflezen in de ijkgrafiek levert een vulstand van 45%
| inzicht dat geldt $T=\frac{benodigde\,\,tijd}{aantal\,\,trillingen}$ en gebruik van $f=\frac{1}{T}$ | 1 punt |
| aflezen van de bijbehorende vulstand | 1 punt |
| completeren van de bepaling en significantie | 1 punt |
Bronvermelding:
- Figuur 1: Shutterstock 144992224 door Tab62
