Examenopgave VWO, natuurkunde, voorbeeldexamen 2016, opgave 1: Rekstrookje

Bron: Wikimedia Commons
Om te controleren of een brug niet te zwaar belast wordt, maakt men gebruik van sensoren. In zo’n sensor zit een zogenoemd ‘rekstrookje’, dat op een kabel van de brug is geplakt. In het rekstrookje is een lange, dunne constantaandraad verwerkt. Zie figuur 1.
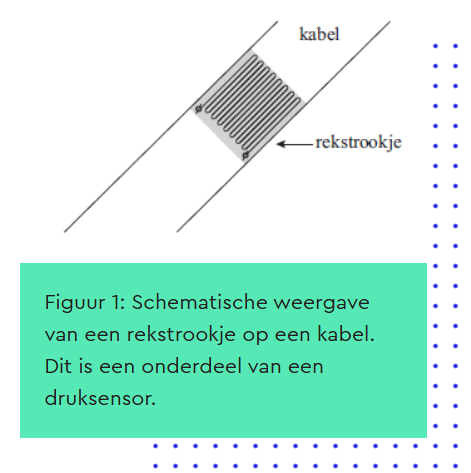
Deze draad heeft een weerstand van 350 Ω en een diameter van 40 μm.
Vraag a. Bereken de lengte van de constantaandraad.
Voor de weerstand geldt:
$R = \rho \frac{l}{A} \text{ met } A = \pi r^{2}$
Omschrijven geeft:
$l = \frac{R \pi r^{2}}{\rho}$
Door waarden in te vullen is de lengte nu te berekenen:
$l = \frac{350 \cdot \pi \cdot (\frac{1}{2} \cdot 40 \cdot 10^{-6})^{2}}{0,\!45 \cdot 10^{-6}} = 0,\!98 \text{ m}$
Als er veel verkeer op de brug is, rekt de kabel een beetje uit. Het rekstrookje rekt relatief evenveel uit. Bij de uitrekking verandert de weerstand van het rekstrookje. Door de weerstandsverandering te meten, weet men of de kabel te veel uitrekt.
Als het rekstrookje uitrekt, wordt de weerstand van de constantaandraad groter.
Vraag b. Geef hier twee redenen voor.
Als het rekstrookje uitrekt, wordt l groter en A kleiner. (Hierdoor wordt R groter.)
De weerstandsverandering van het rekstrookje kan bepaald worden met de schakeling van figuur 2. Als de weerstand van het rekstrookje 1,0 Ω groter wordt, verandert de spanning die de spanningsmeter aangeeft minder dan een half procent.

Vraag c. Toon dit aan.
Als de beide weerstanden gelijk zijn aan 350 Ω, is de spanning die de voltmeter aangeeft gelijk aan 2,50 V.
Als de weerstand van het rekstrookje toeneemt met 1,0 Ω, geldt voor de spanning die de spanningsmeter aangeeft:
$U_{\text{nieuw}} = \frac{350}{701} \cdot 5,\!00 = 2,\!4964 \text{ V}$
Dit is een verschil van 0.0036 V en dit is gelijk aan:
$\frac{0,\!0036}{2,\!50} \cdot 100 \% = 0,\!14 \% < 0,\!5 \%$
Om de weerstandsverandering nauwkeuriger te meten, wordt de schakeling van figuur 3 gebruikt.

Als het rekstrookje niet is uitgerekt en een weerstand heeft van 350 Ω, geeft de microampèremeter 0,000 μA aan.
Als het rekstrookje uitrekt en de weerstand dus groter wordt, gaat er een stroom lopen door de microampèremeter. Dit is te verklaren met behulp van de wetten van Kirchhoff.
Vraag d. Leg uit, gebruik makend van de wetten van Kirchhoff, in welke richting de stroom dan loopt: Van A naar B of van B naar A.
Als het rekstrookje niet uitrekt, is R1 gelijk aan R2 en R3 is gelijk aan R4.
Dus geldt: UAC = UAD = UCB = UBD = 2,50 V.
Als de weerstand van het rekstrookje groter wordt, wordt de spanning over het rekstrookje, UAC, groter.
De spanningswet van Kirchhoff zegt voor kring ACB dat de som van de
spanningen gelijk is aan nul. Oftewel: UCA = UCB + UBA.
Omdat UBA = 0 volgt: UCA = UCB .
Omdat UAC groter wordt, moet UCB groter worden. Dit kan alleen als de stroomsterkte door R4 kleiner wordt dan de stroomsterkte door R3: IBD < ICB.
De stroomwet van Kirchhoff zegt voor punt B dat de ingaande stroom gelijk is aan de uitgaande stroom.
Oftewel: ICB = IBA + IBD.
Doordat IBD < ICB geldt IBA > 0. Dus de stroom gaat van B naar A.
